У якому вона набуває нульового значення. Наприклад, для функції , заданої формулою
Є нулем, оскільки
.Нулі функції також називаються корінням функції.
Поняття нулів функції можна розглядати для будь-яких функцій, область значень яких містить нуль або нульовий елемент відповідної структури алгебри.
Для функції дійсного змінного нулями є значення, у яких графік функції перетинає вісь абсцис.
Знаходження нулів функції найчастіше вимагає використання чисельних методів (наприклад, метод Ньютона, градієнтні методи).
Однією з невирішених математичних проблем є знаходження нулів дзета-функції Рімана.
Корінь багаточлена
Див. також
Література
Wikimedia Foundation. 2010 .
Дивитись що таке "Нуль функції" в інших словниках:
Точка, де задана функція f (z) перетворюється на нуль; таким чином, Н. ф. f (z) це те саме, що й коріння рівняння f(z) = 0. Наприклад, точки 0, π, π, 2π, 2π,... суть нулі функції sinz. Нулі аналітичної функції.
Нуль функція, нуль функції … Орфографічний словник-довідник
Цей термін має й інші значення, див. Нуль. Необхідно перенести вміст цієї статті до статті «Нуль функції». Ви можете допомогти проекту, поєднавши статті. У разі потреби обговорення доцільності об'єднання, замініть цей … Вікіпедія
Або C рядок (від назви мови Сі) або ASCIZ рядок (від назви директиви асемблера.asciz) спосіб подання рядків у мовах програмування, при якому замість введення спеціального рядкового типу використовується масив символів, а кінцем… … Вікіпедія
У квантовій теорії поля прийнята (жаргонне) назва для властивості звернення в нуль фактора перенормування константизв'язку де g0 затравальна константа зв'язку з лагранжіана взаємодії, фіз. константа зв'язку, одягнена взаємодією. Рівність Z … Фізична енциклопедія
Нуль-мутація н-аллель- Нуль мутація, зв. аллель * нуль мутація, н. алель * null mutation або n. allel or silent a. мутація, що веде до повної втрати функції у тій послідовності ДНК, в якій вона відбулася. Генетика. Енциклопедичний словник
Твердження теоретично ймовірностей у тому, що будь-яка подія (т. зв. залишкова подія), наступ до рого визначається лише скільки завгодно віддаленими елементами послідовності незалежних випадкових подій чи випадкових величин, має… Математична енциклопедія
1) Число, що володіє тим властивістю, що будь-яке (дійсне або комплексне) число при складанні з ним не змінюється. Позначається символом 0. Добуток будь-якого числа на Н. дорівнює Н.: Якщо добуток двох чисел дорівнює Н., то один із співмножників … Математична енциклопедія
Функції, задані співвідношеннями між незалежними змінними, не дозволеними щодо останніх; ці співвідношення є одним із способів завдання функції. Наприклад, співвідношення x2 + y2 1 = 0 задає Н. ф. … Велика Радянська Енциклопедія
Математичне уявлення функції показує наочно те, як одна величина повністю визначає значення іншої величини. Традиційно розглядаються числові функції, які ставлять у відповідність одним числам інші. Нулем функції, зазвичай називають значення аргументу, у якому функція перетворюється на нуль.
Інструкція
1. Для того, щоб знайти нулі функції, необхідно прирівняти її праву частину до нуля і вирішити отримане рівняння. Припустимо, вам дана функція f(x) = x-5.
2. Для знаходження нулів цієї функції, візьмемо та прирівняємо її праву частину до нуля: x-5=0.
3. Вирішивши це рівняння отримаємо, що x=5 і це значення аргументу і буде нулем функції. Тобто за значення доводу 5, функція f(x) звертається в нуль.
Під поданням функціїу математиці розуміють зв'язок між елементами множин. Якщо говорити більше вірно, це «закон», за яким усьому елементу однієї множини (званої областю визначення) ставиться у відповідність певний елемент іншої множини (званої областю значень).

Вам знадобиться
- Знання в галузі алгебри та математичного огляду.
Інструкція
1. Значення функціїце певна область, значення з якої може набувати функції. Скажімо область значення функції f(x)=|x| від 0 до нескінченності. Щоб виявити значення функціїу певній точці потрібно підставити замість доказу функціїйого числовий еквівалент, отримане число і буде значенням функції. Нехай дана функція f(x)=|x| - 10 + 4x. Виявимо значення функціїу точці x=-2. Підставимо замість x число -2: f(-2)=|-2| - 10 + 4 * (-2) = 2 - 10 - 8 = -16. Тобто значення функціїу точці -2 і -16.
Зверніть увагу!
Перш ніж шукати значення функції у точці – переконайтеся, що вона входить у область визначення функції.
Корисна порада
Аналогічним способом можна знайти значення функції кількох аргументів. Відмінність у цьому, замість одного числа потрібно буде підставити кілька – за кількістю доводів функції.
Функція являє собою встановлену зв'язаність змінної у змінної x. Причому всім значенням х, званого доказом, відповідає виняткове значення у функції. У графічному вигляді функція зображується на системі декартової координат у вигляді графіка. Точки перетину графіка з віссю абсцис, де відкладаються докази х, називаються нулями функції. Пошук допустимих нулів – одне із завдань з пошуку заданої функції. При цьому враховуються всі допустимі значення самостійної змінної x, що утворюють область визначення функції (ОФ).

Інструкція
1. Нуль функції – це значення доводу х, у якому значення функції дорівнює нулю. Втім нулями можуть бути ті докази, які входять у область визначення досліджуваної функції. Тобто в таке безліч значень, для яких функція f (x) має толк.
2. Запишіть задану функцію і прирівняйте її до нуля, скажімо f(x) = 2х?+5х+2 = 0. Розв'яжіть рівняння, що вийшло, і виявте його дійсне коріння. Коріння квадратного рівняння обчислюється за допомогою знаходження дискримінанта. 2х?+5х+2 = 0; D = b?-4ac = 5?-4 * 2 * 2 = 9; х1 = (-b +? = -0,5; х2 = (-b-?D) / 2 * а = (-5-3) / 2 * 2 = -2. f(x).
3. Усі виявлені значення x перевірте на належність до області визначення заданої функції. Виявіть ООФ, при цьому перевірте початковий вираз наявність коренів парної ступеня виду?f (х), наявність дробів у функції з доказом у знаменнику, наявність логарифмічних чи тригонометрических выражений.
4. Розглядаючи функцію з виразом під коренем парного ступеня, прийміть за область визначення всі докази х, значення яких не перетворюють підкорене вираз у негативне число (навпаки функція не має сенсу). Уточніть, чи випадають виявлені нулі функції в певну область допустимих значень х.
5. Знаменник дробу не може звертатися в нуль, тому виключіть ті аргументи х, які призводять до такого результату. Для логарифмічних величин слід розглядати ті значення доводу, у яких саме вираз величезніше нуля. Нулі функції, що обертають подлогарифмическое вираз у нуль чи негативне число, би мало бути відкинуті з фінального результату.
Зверніть увагу!
При знаходження коренів рівняння, можуть виникнути зайві корені. Перевірити це легко: досить підставити отримане значення доводу в функцію і переконатися чи функція обертається в нуль.
Корисна порада
Зрідка функція не виявляється у очевидному вигляді через свій аргумент, тоді легко потрібно знати, що являє собою ця функція. Прикладом цього може бути рівняння кола.
2. Знайдемо нулі функції.
f(x) при х ![]() .
.
Відповідь f(x) при х ![]() .
.
2) х 2 >-4x-5;
x 2+4x+5>0;
Нехай f(x)=х 2 +4х +5 тоді Знайдемо такі х за яких f(x)>0,
D=-4 Немає нулів.

4. Системи нерівностей. Нерівності та системи нерівностей із двома змінними
1) Безліч рішень системи нерівностей є перетин множини рішень нерівностей, що входять до неї.
2) Безліч розв'язків нерівності f(х;у)>0 можна графічно зобразити на координатній площині. Зазвичай лінія, задана рівнянням f(х; у) = 0, розбиває площину на 2 частини, одна з яких є розв'язком нерівності. Щоб визначити, яка частина, треба підставити координати довільної точки М(х0;у0) , що не лежить на лінії f(х;у)=0, в нерівність. Якщо f(х0;у0) > 0 то рішенням нерівності є частина площини, що містить точку М0. якщо f(х0; у0)<0, то другая часть плоскости.
3) Безліч рішень системи нерівностей є перетин множини рішень нерівностей, що входять до неї. Нехай, наприклад, задана система нерівностей:
 .
.
Для першої нерівності безліч розв'язків є коло радіусом 2 і з центром на початку координат, а для другого - напівплощина, розташована над прямою 2х+3у=0. Безліч рішень цієї системи служить перетинання зазначених множин, тобто. півколо.
4) Приклад. Вирішити систему нерівностей:

Рішенням 1-ї нерівності служить безліч, 2-го безліч (2; 7) і третьої - безліч.
Перетином зазначених множин є проміжок (2; 3), який і є безліч розв'язків системи нерівностей.
5. Вирішення раціональних нерівностей методом інтервалів
В основі методу інтервалів лежить наступна властивість двочлена (х-а): точка х = α ділить числову вісь на дві частини - праворуч від точки α двочлен (х-α)> 0, а зліва від точки α (х-α)<0.
Нехай потрібно вирішити нерівність (x-α 1)(x-α 2)...(x-α n)>0, де α 1 , α 2 ...α n-1 , α n - фіксовані числа, серед яких немає рівних, причому такі, що α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 методом інтервалів надходять наступним чином: на числову вісь наносять числа 1, 2 ... n-1, n; у проміжку праворуч від найбільшого їх, тобто. числа ? Тоді безліч усіх розв'язків нерівності (x-α 1)(x-α 2)...(x-α n)>0 буде об'єднання всіх проміжків, у яких поставлено знак «плюс», а безліч розв'язків нерівності (x-α 1 )(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».
1) Вирішення раціональних нерівностей (тобто нерівностей виду ![]() P(x) Q(x) де – багаточлени) засновано на наступній властивості безперервної функції: якщо безперервна функція перетворюється на нуль у точках х1 і х2 (х1;х2) і між цими точками не має інших коренів, то в проміжках(х1; х2) функція зберігає свій знак.
P(x) Q(x) де – багаточлени) засновано на наступній властивості безперервної функції: якщо безперервна функція перетворюється на нуль у точках х1 і х2 (х1;х2) і між цими точками не має інших коренів, то в проміжках(х1; х2) функція зберігає свій знак.
Тому для знаходження проміжків знаковості функції y=f(x) на числовій прямій відзначають усі точки, в яких функція f(x) звертається в нуль або зазнає розриву. Ці точки розбивають числову пряму кілька проміжків, всередині кожного у тому числі функція f(x) безперервна і звертається у нуль, тобто. зберігає знак. Щоб визначити цей знак, достатньо знайти знак функції в будь-якій точці проміжку числової прямої.
2) Для визначення інтервалів знаковості раціональної функції, тобто. Для вирішення раціональної нерівності, відзначаємо на числовому прямому корені чисельника і корені знаменника, які як і є корінням і точками розриву раціональної функції.
Розв'язання нерівностей методом інтервалів
3. ![]() < 20.
< 20.
Рішення. Область допустимих значень визначається системою нерівностей:
Для функції f(x) = ![]() – 20. Знаходимо f(x):
– 20. Знаходимо f(x):

звідки x = 29 та x = 13.
f(30) = - 20 = 0,3> 0,
f(5) = - 1 - 20 = - 10< 0.
Відповідь: . Основні методи розв'язання раціональних рівнянь. 1) Найпростіші: вирішуються шляхом звичайних спрощень - приведення до спільного знаменника, приведення подібних членів тощо. Квадратні рівняння ax2 + bx + c = 0 вирішуються за допомогою...
X змінюється на проміжку (0,1], і зменшується на проміжку = ½ [  -(1/3)
-(1/3) ], за | z|<
1.
], за | z|<
1.
b) f(z)
= - ½ [  +
+ ]
= -
(
]
= -
( ), при 1< |z|
< 3.
), при 1< |z|
< 3.
с) f(z)
=
½ [  ]= -
½
[
]= -
½
[  ]
=
]
=
=
- ½
= -
 , при | 2 - z|
< 1
, при | 2 - z|
< 1
Це коло радіуса 1 з центром у точці z = 2 .
У ряді випадків статечні ряди можна звести до набору геометричних прогресій і після цього легко визначити область їхньої збіжності.
Пр. Дослідити збіжність ряду
.
. . +
 +
+
 +
+
 +
1
+ ()
+ ()
2
+ ()
3
+ . . .
+
1
+ ()
+ ()
2
+ ()
3
+ . . .
Рішення. Це сума двох геометричних прогресій з q 1
=
 , q 2 = (). З умов їх збіжності випливає
, q 2 = (). З умов їх збіжності випливає  < 1 ,
< 1 ,
 < 1 или |z|
> 1 , |z|
< 2 , т.е. область сходимости ряда кольцо
1 < |z|
< 2 .
< 1 или |z|
> 1 , |z|
< 2 , т.е. область сходимости ряда кольцо
1 < |z|
< 2 .
Функція- Це одне з найважливіших математичних понять. Функція - залежність змінної увід змінної xякщо кожному значенню хвідповідає єдине значення у. Змінну хназивають незалежною змінною чи аргументом. Змінну уназивають залежною змінною. Усі значення незалежної змінної (змінної x) утворюють область визначення функції. Усі значення, які набуває залежна змінна (змінна y), утворюють область значень функції.
Графіком функціїназивають безліч всіх точок координатної площини, абсциси яких рівні значенням аргументу, а ординати - відповідним значенням функції, тобто по осі абсцис відкладаються значення змінної x, а по осі ординат відкладаються значення змінної y. Для побудови графіка функції потрібно знати характеристики функції. Основні характеристики функції будуть розглянуті далі!
Для побудови графіка функції радимо використовувати нашу програму - Побудова графіків функцій онлайн. Якщо під час вивчення матеріалу на даній сторінці у Вас виникнуть запитання, Ви завжди можете задати їх на нашому форумі. Також на форумі Вам допоможуть вирішити завдання з математики, хімії, геометрії, теорії ймовірності та багатьох інших предметів!
Основні характеристики функцій.
1) Область визначення функції та область значень функції.
Область визначення функції - це безліч всіх допустимих дійсних значень аргументу x(змінною x), при яких функція y = f(x)визначено.
Область значень функції - це безліч усіх дійсних значень y, що приймає функцію.
В елементарної математики вивчаються функції лише з безлічі дійсних чисел.
2) Нулі функції.
Нуль функції – таке значення аргументу, у якому значення функції дорівнює нулю.
3) Проміжки знаковості функції.
Проміжки знакостійності функції – такі безлічі значень аргументу, у яких значення функції лише позитивні чи лише негативні.
4) Монотонність функції.
Зростаюча функція (у певному проміжку) — функція, яка має більшому значенню аргументу з цього проміжку відповідає більше значення функції.
Зменшена функція (у певному проміжку) — функція, яка має більшому значенню аргументу з цього проміжку відповідає менше значення функції.
5) парність (непарність) функції.
Четна функція — функція, у якої область визначення симетрична щодо початку координат та для будь-якого хв галузі визначення виконується рівність f(-x) = f(x). Графік парної функції симетричний щодо осі ординат.
Непарна функція — функція, у якої область визначення симетрична щодо початку координат та для будь-якого хв галузі визначення справедлива рівність f(-x) = - f(x). Графік непарної функції симетричний щодо початку координат.
6) Обмежена та необмежена функції.
Функція називається обмеженою, якщо є таке позитивне число M, що |f(x)| ≤ M для всіх значень x. Якщо такої кількості немає, то функція — необмежена.
7) Періодичність функції.
Функція f(x) — періодична, якщо є таке відмінне від нуля число T, що з будь-якого x f(x+T) = f(x). Таке найменше називається періодом функції. Усі тригонометричні функції є періодичними. (Тригонометричні формули).
Вивчивши дані властивості функції, Ви без проблем зможете дослідити функцію і за властивостями функції зможете побудувати графік функції. Також подивіться матеріал про таблицю істинності, таблицю множення, таблицю Менделєєва, таблицю похідних та таблицю інтегралів.
Нулі функції
Що таке нулі? Як визначити нулі функції аналітично та за графіком?
Нулі функції- це значення аргументу, у яких функція дорівнює нулю.
Щоб знайти нулі функції, заданої формулою y=f(x), треба розв'язати рівняння f(x)=0.
Якщо рівняння немає коренів, нулів функції немає.
1) Знайти нулі лінійної функції y=3x+15.
Щоб знайти нулі функції, розв'яжемо рівняння 3x+15 =0.
Отже, нуль функції y=3x+15 - x= -5 .
2) Знайти нулі квадратичної функції f(x)=x²-7x+12.
Для знаходження нулів функції розв'яжемо квадратне рівняння
Його коріння x1=3 та x2=4 є нулями цієї функції.
3) Знайти нулі функції
Дроб має сенс, якщо знаменник відмінний від нуля. Отже, x²-1≠0, x²≠1,x≠±1. Тобто область визначення цієї функції (ОДЗ)
![]()
З коренів рівняння x²+5x+4=0 x1=-1 x2=-4 область визначення входить тільки x=-4.
Щоб знайти нулі функції, заданої графічно, потрібно знайти точки перетину графіка функції з віссю абсцис.
Якщо графік не перетинає вісь Ox, функція не має нулів.

функція, графік якої зображений на малюнку, має чотири нулі -
В алгебрі завдання знаходження нулів функції зустрічається як у вигляді самостійного завдання, так і при вирішенні інших завдань, наприклад, при дослідженні функції, розв'язанні нерівностей тощо.
www.algebraclass.ru
Правило нулі функції

![]()
![]()
Основні поняття та властивості функцій
Правило (Закон) відповідності. Монотонна функція .
Обмежена та необмежена функції. Безперервна та
розривна функції . Парна та непарна функції.
Періодична функція. Період функції.
Нулі функції . Асимптота .
Область визначення та область значень функції. В елементарній математиці вивчаються функції лише на безлічі дійсних чисел R . Це означає, що аргумент функції може набувати ті дійсні значення, у яких функція визначена, т. е . вона також набуває лише дійсних значень. Безліч X всіх допустимих дійсних значень аргументу x, при яких функція y = f (x) визначена, називається областю визначення функції. Безліч Y всіх дійсних значень y, які приймає функція, називається областю значень функції. Тепер можна надати більш точне визначення функції: правило (закон) відповідності між множинами Xі Y , за яким для кожного елемента з множини Xможна знайти один і тільки один елемент з множини Yназивається функцією .
З цього визначення випливає, що функція вважається заданою, якщо:
- задана область визначення функції X ;
- задана область значень функції Y ;
- Відомо правило (закон) відповідності, причому таке, що для кожного
значення аргументу може бути знайдено лише одне значення функції.
Ця вимога однозначності функції є обов'язковою.

Монотонна функція.
Якщо для будь-яких двох значень аргументу x 1 та x 2 з умови x 2 > x 1 слід f (x 2) > f (x 1), то функція f (x) називається зростаючою; якщо для будь-яких x 1 та x 2 з умови x 2 > x 1 слід f (x 2) 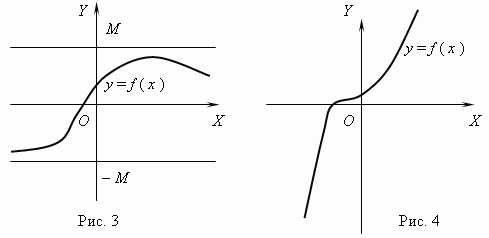
Функція, зображена на рис.3 є обмеженою, але не монотонною. Функція на рис.4 - саме навпаки, монотонна, але необмежена. (Поясніть це, будь ласка!).
Безперервна та розривна функції. Функція y = f (x) називається безперервний у точці x = a, якщо:
1) функція визначена при x = aт. e. f (a) існує;
2) існує кінцевиймежа lim f (x) ;
Якщо не виконується хоча б одна з цих умов, то функція називається розривнийу точці x = a .
Якщо функція безперервна у всіх точках своєї галузі визначення, то вона називається безперервною функцією.

Парна та непарна функції. Якщо для будь-якого xв галузі визначення функції має місце: f (— x) = f (x), то функція називається парної; якщо має місце: f (— x) = — f (x), то функція називається непарний. Графік парної функції симетричний щодо осі Y(рис.5), a графік непарної функції цим метричний щодо початку координат(Рис.6).
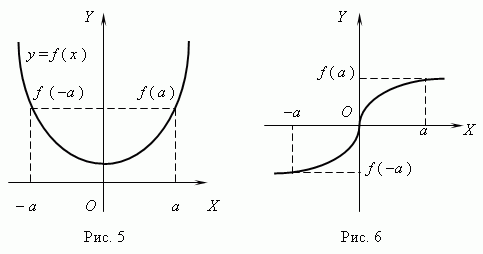
Періодична функція. Функція f (x) — періодичнаякщо існує таке відмінне від нулячисло T, що для будь-якого xв галузі визначення функції має місце: f (x + T) = f (x). Таке найменшечисло називається періодом функції. Усі тригонометричні функції є періодичними.
П р і м е р 1 . Довести, що sin xмає період 2 .
Рішення. Ми знаємо, що sin ( x + 2 n) = sin x, де n= 0, ± 1, ± 2, …
Отже, додавання 2 nдо аргументу синуса не
змінює його значення e. Чи існує інше число з таким
Припустимо, що P- Таке число, тобто e. рівність:
справедливо для будь-якого значення x. Але тоді воно має
місце і при x= / 2, тобто e.
sin (/ 2 + P) = sin / 2 = 1.
Але за формулою приведення sin (/2 + P) = cos P. Тоді
з двох останніх рівностей випливає, що cos P= 1, але ми
знаємо, що це правильно лише за P = 2 n. Оскільки найменшим
відмінним від нуля числом із 2 nє 2 , то це число
і є період sin x. Аналогічно доводиться, що 2
є періодом і для cos x .
Доведіть, що функції tan xта cot xмають період.
П р і м е р 2. Яка кількість є періодом функції sin 2 x ?
Розв'яжемо sin 2 x= sin (2 x + 2 n) = sin [ 2 ( x + n) ] .
Ми бачимо, що додавання nдо аргументу x, не змінює
значення функції. Найменше відмінне від нуля число
з nє , таким чином, це період 2 x .
Нулі функції. Значення аргументу, у якому функція дорівнює 0, називається нулем ( коренем) функції. Функція може мати кілька нулів. Наприклад, функція y = x (x + 1) (x- 3) має три нулі: x = 0, x = — 1, x= 3. Геометрично нуль функції – це абсциса точки перетину графіка функції з віссю Х .
На рис.7 представлений графік функції з нулями: x = a , x = bі x = c .
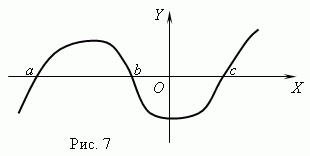
Асимптота. Якщо графік функції необмежено наближається до деякої прямої при віддаленні від початку координат, то ця пряма називається асимптотою.
Тема 6. "Метод інтервалів".
Якщо f (x) f (x 0) при х х 0 то функцію f (x) називають безперервний у точці х 0.
Якщо функція безперервна в кожній точці деякого проміжку I, то її називають безперервний на проміжку I (проміжок I називають проміжком безперервності функції). Графік функції на цьому проміжку є безперервною лінією, про яку говорять, що її можна «намалювати, не відриваючи олівця від паперу».
Властивість безперервних функцій.
Якщо на інтервалі (a ; b) функція f неперервна і не перетворюється на нуль, то вона на цьому інтервалі зберігає постійний знак.
У цьому властивості заснований спосіб розв'язання нерівностей з однієї змінної – спосіб інтервалів. Нехай функція f(x) безперервна на інтервалі I і перетворюється на нуль у кінцевому числі точок цього інтервалу. За якістю безперервних функцій цими точками I розбивається на інтервали, у кожному їх безперервна функція f(x) c охороняє постійний знак. Щоб визначити цей знак, достатньо обчислити значення функції f(x) в одній точці з кожного такого інтервалу. Виходячи з цього, отримаємо наступний алгоритм розв'язання нерівностей методом інтервалів.
Метод інтервалів для нерівностей виду
Метод інтервалів. Середній рівень.
Хочеш перевірити свої сили та дізнатися про результат наскільки ти готовий до ЄДІ чи ОДЕ?
Лінійна функція
Лінійною називається функція виду. Розглянемо для прикладу функцію. Вона позитивна при 3 і негативна при. Крапка – нуль функції (). Покажемо знаки цієї функції на числовій осі:
Говоримо, що «функція змінює знак під час переходу через точку».
Видно, що знаки функції відповідають положенню графіка функції: якщо графік вищий за осі, знак « », якщо нижче – « ».
Якщо узагальнити отримане правило довільну лінійну функцію, отримаємо такий алгоритм:
Квадратична функція
Сподіваюся, ти пам'ятаєш, як вирішуються квадратні нерівності? Якщо ні, прочитай тему «Квадратні нерівності». Нагадаю загальний вигляд квадратичної функції: .
Тепер згадаємо, які знаки набуває квадратична функція. Її графік – парабола, і функція приймає знак « » при таких, при яких парабола вища за осі, і « » – якщо парабола нижче за осю:
Якщо функція має нулі (значення, при яких), парабола перетинає вісь у двох точках – коренях відповідного квадратного рівняння. Таким чином вісь розбивається на три інтервали, а знаки функції змінюються поперемінно при переході через кожен корінь.
А чи можна якось визначити знаки, не малюючи щоразу параболу?
Згадаймо, що квадратний тричлен можна розкласти на множники:
Відзначимо коріння на осі:
Ми пам'ятаємо, що знак функції може змінюватись лише при переході через корінь. Використовуємо цей факт: для кожного з трьох інтервалів, на які вісь розбивається корінням, достатньо визначити знак функції лише в одній довільно вибраній точці: в інших точках інтервалу знак буде таким самим.
У нашому прикладі: при 3″ обидва вирази у дужках позитивні (підставимо, наприклад: 0″). Ставимо на осі знак « »:
Ну і, при (підстав, наприклад,) обидві дужки негативні, отже, твір позитивно:
Це і є метод інтервалів: знаючи знаки співмножників на кожному інтервалі, визначаємо знак всього твору
Розглянемо також випадки, коли нулів у функції немає, або він лише один.
Якщо їх немає, то й коріння немає. А отже, не буде й «переходу через корінь». Отже, функція по всій числової осі приймає лише одне знак. Його легко визначити, підставивши функцію.
Якщо корінь лише один, парабола стосується осі, тому знак функції не змінюється під час переходу через корінь. Яке правило вигадаємо для таких ситуацій?
Якщо розкласти таку функцію на множники, вийдуть два однакові множники:
А будь-який вираз у квадраті невід'ємний! Тому знак функції не змінюється. У таких випадках виділятимемо корінь, при переході через який знак не змінюється, обвівши його квадратиком:
Таке коріння називатимемо кратним.
Метод інтервалів у нерівностях
Тепер будь-яку квадратну нерівність можна вирішувати без малювання параболи. Достатньо лише розставити на осі знаки квадратичної функції і вибрати інтервали в залежності від знаку нерівності. Наприклад:
Відміряємо коріння на осі і розставимо знаки:
Нам потрібна частина осі зі знаком «»; оскільки нерівність несувора, саме коріння теж включаються до рішення:
Тепер розглянемо раціональну нерівність – нерівність, обидві частини якої є раціональними виразами (див. «Раціональні рівняння»).
Приклад:
Всі множники крім одного – тут «лінійні», тобто містять змінну лише в першому ступені. Такі лінійні множники нам і потрібні для застосування методу інтервалів – знак при переході через їхнє коріння змінюється. А ось множник взагалі не має коріння. Це означає, що він завжди позитивний (перевір це сам), і тому не впливає на знак усієї нерівності. Отже, на нього можна поділити ліву та праву частину нерівності, і таким чином позбутися її:
Тепер так само, як було з квадратними нерівностями: визначаємо, в яких точках кожен з множників звертається в нуль, відзначаємо ці точки на осі і розставляємо знаки. Звертаю увагу дуже важливий факт:
У разі парної кількості чинимо так само, як і раніше: обводимо крапку квадратиком і не міняємо знак при переході через корінь. А от у разі непарної кількості це правило не виконується: знак все-одно зміниться при переході через корінь. Тому з таким корінням нічого додатково не робимо, начебто він у нас не кратний. Вищеописані правила відносяться до всіх парних і непарних ступенів.
Що запишемо у відповіді?
При порушенні чергування знаків потрібно бути дуже уважним, адже за несуворої нерівності у відповідь повинні увійти всі зафарбовані точки. Але деякі з нас часто стоять особняком, тобто не входять у зафарбовану область. У цьому випадку ми додаємо їх до відповіді як ізольовані точки (у фігурних дужках):
Приклади (виріши сам):
Відповіді:
- Якщо серед множників просто це корінь, адже його можна уявити як.
.


